📌Metas

Overview

Metas are categories of things available in the Google Street View imagery used by GeoGuessr that can be used to arrive at a guess about where in this wide world you were dropped at the start of the round. While it’s debatable whether metas like the generation or type of camera or the specific cars used to capture Street View images is in the true “spirit” of the game since they don’t really relate directly to geographical knowledge, anything that can be seen and recognized in these images can potentially provide information that a player with the right knowledge might use to their advantage. The top-level (📌) page for each meta contains a description and various information about the meta (the meta meta, if you will) to help you decide how best, or even whether at all, to learn and employ it.

Why Learn Metas?

Metas provide sets of clues which map to places which can be stacked together to construct a guess. When you recognize a specific meta clue it tells you information about where and, as importantly, where not you’re likely to be. Learning metas is how players naturally start improving in the game as it’s, well, just kind of how the game works: you get dropped in a place, you observe some stuff, you form a hypothesis about where you are based on these observations, at the end of the round you’re shown the answer and you update your existing knowledge about what the things you observed mean. The alternative method, studying broad knowledge about specific places, tends to be less efficient at earlier stages of development as it can easily lead to overlearning. Instead, it’s better to start out studying broad metas and just playing the game, letting groups of clues gradually start to mentally “clump” into islands of information related to specific places which you can then later be refined and expanded upon.

Likelihood Vectors

A sophisticated metaphor for meta clues is that of likelihood vectors, sets of values indicating toward or against the likelihood that you are in a place.

For example, consider the driving side meta clue and picture it as a list of numbers representing each country in the world. If you’re dropped in a location and identify it as a left-driving country, the likelihood vector for that meta clue might look like this:

$$DriveSid{e}_{left}=\left[\begin{array}{ccccccccc}\underset{\text{UK}}{+100}& \underset{\text{Ireland}}{+100}& \underset{\text{United States}}{-100}& \underset{\text{Canada}}{-100}& ...& \underset{\text{Australia}}{+100}& \underset{\text{Spain}}{-100}& \underset{\text{Indonesia}}{+100}& \end{array}\right]$$

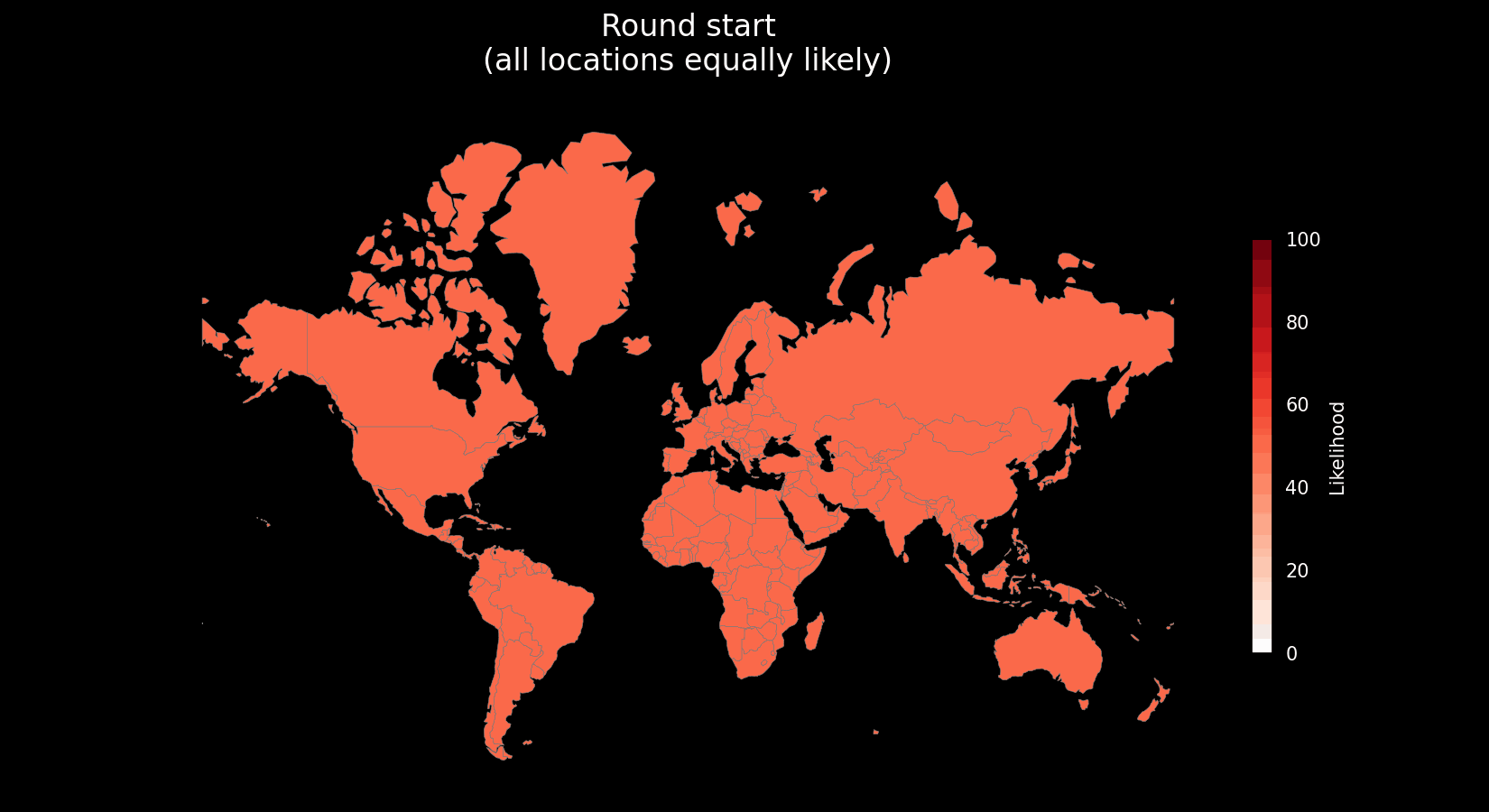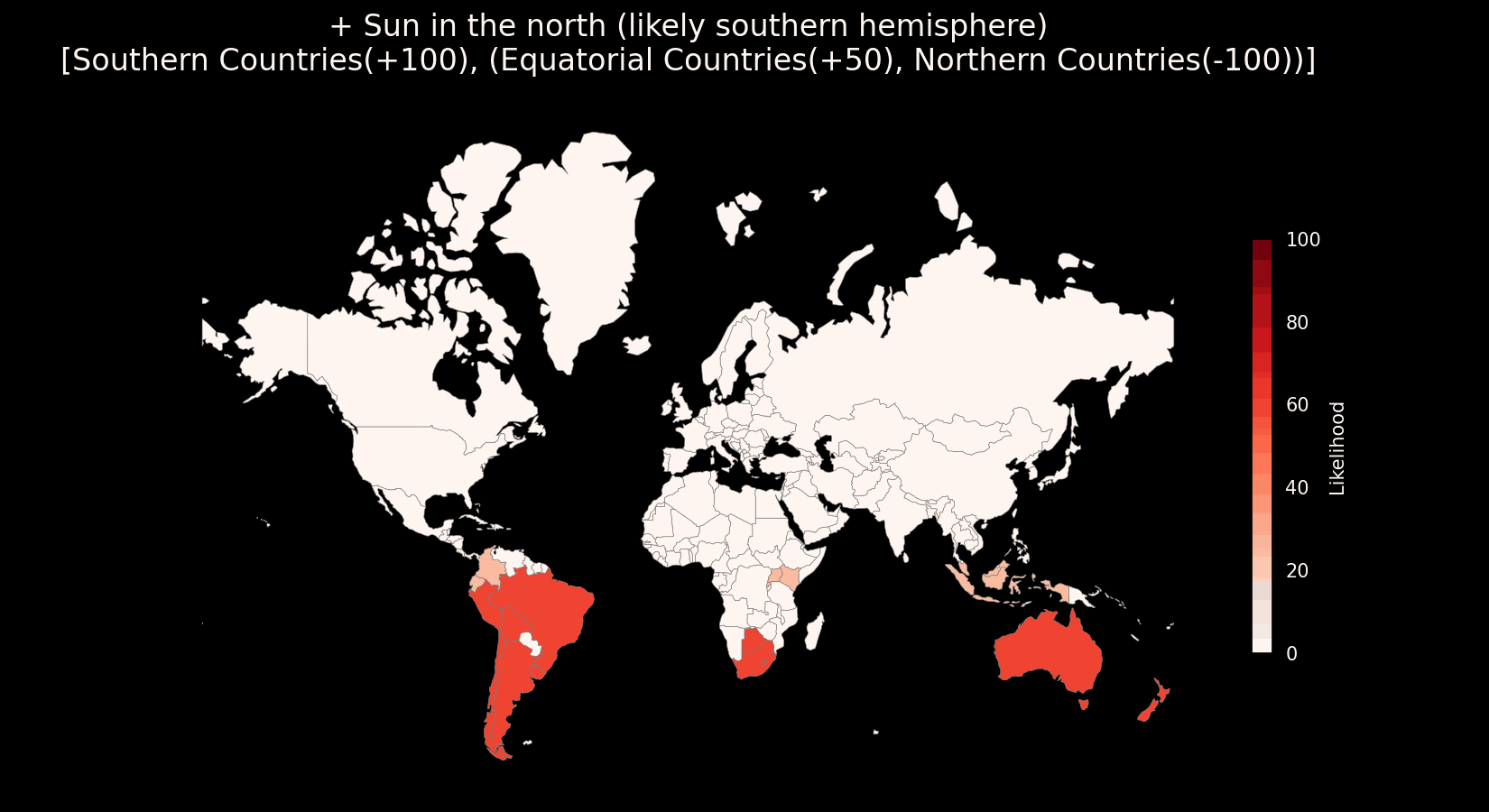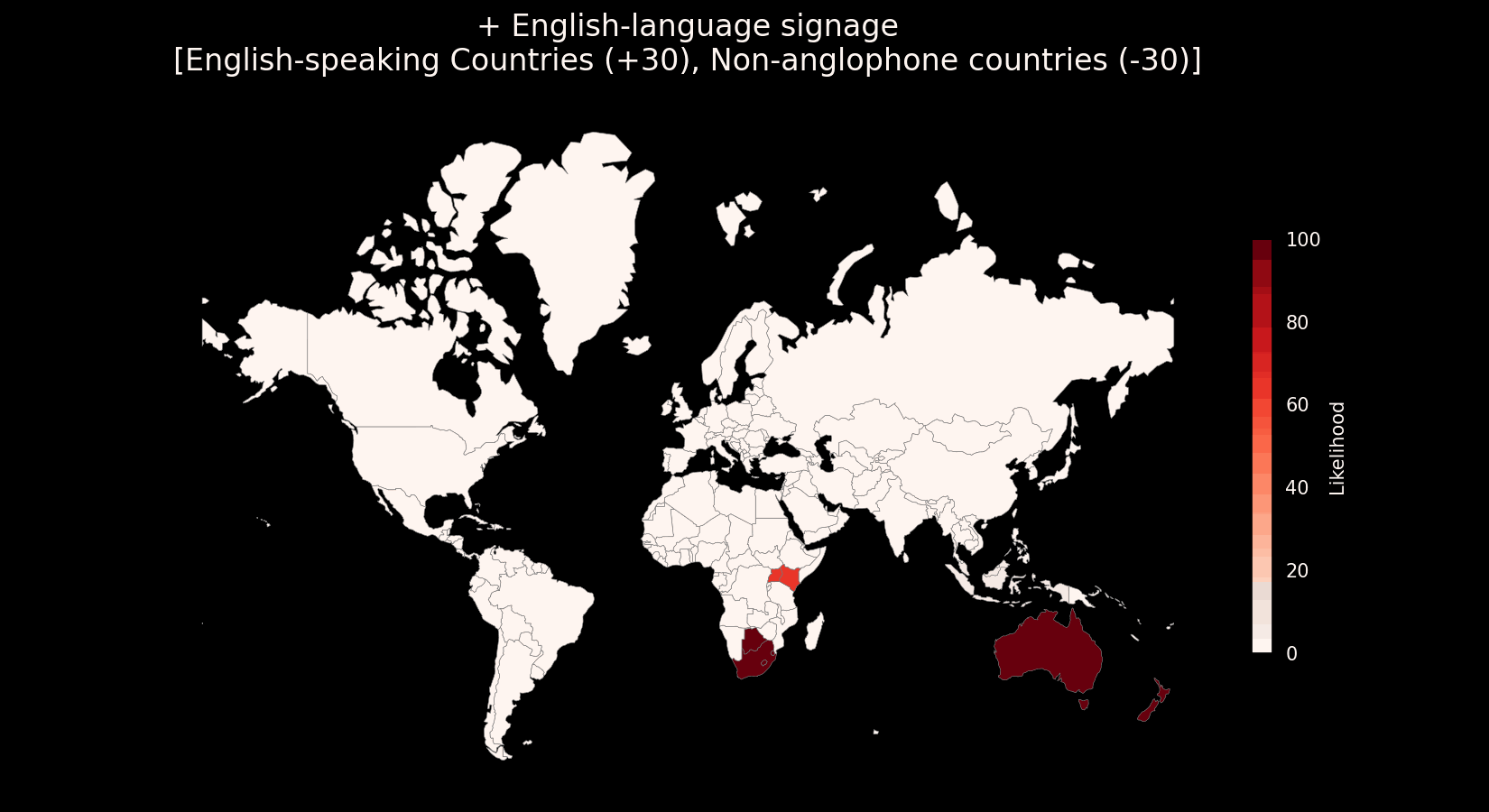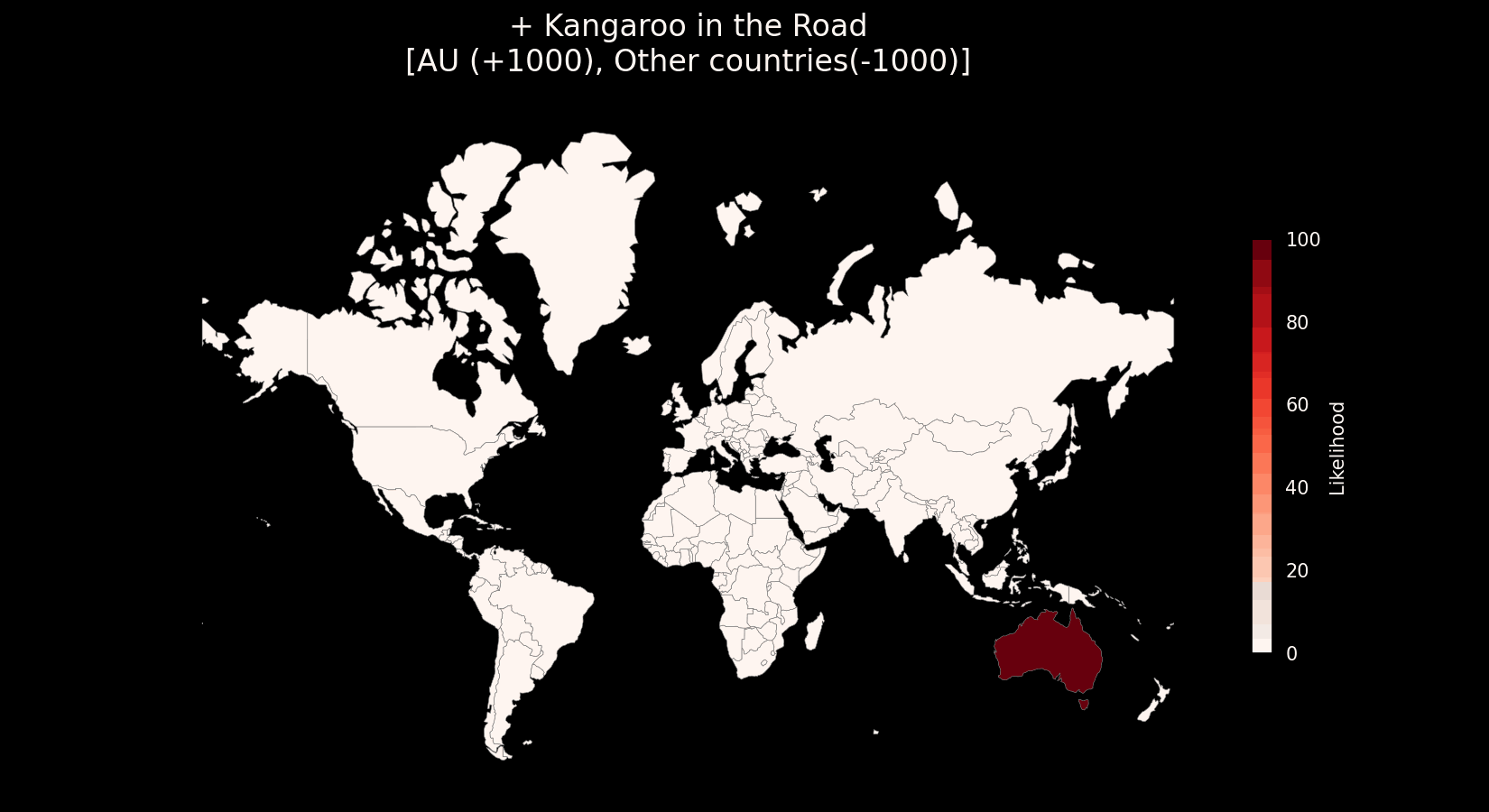
This vector tips the arrow of likelihood strongly away from any right-hand driving countries. Now let’s say that you look around some more and notice that the sun appears to be in the north. This typically indicates that you are in the southern hemisphere but this clue can be deceptive depending on a variety of factors, especially toward the equator, so you might factor in this uncertainty:

$$SunDirectio{n}_{north}=\left[\begin{array}{ccccccccc}\underset{\text{UK}}{-100}& \underset{\text{Ireland}}{-100}& ...& \underset{\text{Ecuador}}{-25}& \underset{\text{Kenya}}{-25}& ...& \underset{\text{Australia}}{+100}& \underset{\text{New Zealand}}{+100}& \end{array}\right]$$

This vector tips your guess strongly toward the southern hemisphere but hedges near the equator by applying a reduced penalty to equatorial countries. As you play and observe, you’re essentially collecting a rolling sum of vectors representing your perceived likelihood for each possible location. As these likelihood values shift, a set of the most likely candidates emerges.

$$\begin{array}{rl}\text{Likelihood}& =DriveSid{e}_{left}+SunDirectio{n}_{north}\\ & \\ & =\left[\begin{array}{cccccccc}\underset{\text{UK}}{-100}& \underset{\text{Ireland}}{-100}& \underset{\text{United States}}{-200}& \underset{\text{Canada}}{-200}& ...& \underset{\text{Australia}}{+200}& \underset{\text{Spain}}{-200}& \underset{\text{Indonesia}}{+75}\end{array}\right]\end{array}$$

Likelihood vectors make a particularly compelling mental model due to their composability, each clue contributes its own “nudge” toward or away from specific places. The more you observe and identify, the more these nudges stack up to shape a confident, refined guess. This mirrors how human reasoning often works: we don’t usually land on an answer all at once, but rather accumulate partial evidence until a pattern emerges strongly enough to act on. They also provide an excellent framework for quantitative analysis of metas (see the next section on meta evaluation).

While we’re calling these “vectors,” it’s worth acknowledging that the real structure of these clues is often more complex. Many metas don’t map cleanly to countries—they might point to regions, states, or even individual cities and are often hierarchical (e.g., a clue that applies to Brazil as a whole but even more strongly to São Paulo), or conditional (e.g., only valid under certain lighting conditions or time periods). From a strict mathematical perspective, this implies something closer to a tensor, a multi-dimensional structure encoding relationships at different levels of granularity.

However, for practical purposes thinking of meta clues as vectors is perfectly sufficient. It allows you to reason incrementally, update guesses intuitively, and avoid getting lost in overly abstract frameworks. As your skills develop, you’ll naturally start to notice and internalize the more layered structure behind these signals, but there’s no need to get bogged down in that complexity from the outset.

Evaluating Metas

In this guide I try to evaluate the in-game utility of metas along some key axes. I lean heavily on the concept of likelihood vectors as it provides a useful framework for applying quantitative methods to these evaluations. Each meta is given a score from 1 to 10 in each of the following domains to help the reader assess which metas to study. Justifications for each score are supplied alongside the scores themselves in the top-level page for the meta.

Note on Meta Granularity

While this guide uses broad meta categories (like “area codes,” “utility poles,” or “bollards”) as top-level entries, many of these are best understood as meta umbrellas — collections of related but independently varying clue systems used across different regions.

As a result, individual clue sets, or “sub-metas,” within an umbrella meta are scored separately. The scores given in top-level meta pages represent weighted averages of these sub-meta scores, with weights based on the geographic size or gameplay frequency of each region.

For example, the area codes meta includes distinct sub-metas for each country’s numbering system. These vary widely in difficulty and usefulness. To wit, Brazilian area codes are geographically regular and easy to learn, while US area codes are wildly irregular and much harder to apply.

Difficulty

Difficulty is a measure of how much work is required to learn and employ a meta effectively and consistently in the game. Key factors that contribute to meta difficulty include:

• Ease of memorization: How many individual clues does the meta consist of and how much do they differ?

  • Examples:
    • The driving sides for each country are much easier to memorize, relatively speaking, as the driving sides meta effectively only has a single, binary clue (right or left) that is applied consistently throughout each country.
    • Area codes are highly complex with potentially hundreds of individual codes (clues) to memorize within a single country.
  • Theoretical metrics:
    • memorization burden = number of unique mappings (clue → region)

• Ease of recognition: How easy are meta clues to notice or identify, typically, in Google Street View coverage?

  • Examples:
    • License plates would be a hugely over-powered meta if they weren’t obscured in Street View with only vague blurs to go off of for the most part.
  • Theoretical metrics:
    • recognition rate = # of panoramas where a specific clue is visible / # of panoramas where a majority of players who know the clue can confidently recognize it

• Ease of discrimination: Sometimes meta clues can look very similar or even identical to one another, leading to confusion and misidentification.

  • Examples:
    • Thai and Khmer scripts can look very similar to the untrained eye.
  • Theoretical metrics:
    • discrimination score = 1 - average false-positive rate across common lookalikes

• Pattern coherence: Basically, how easy is it to memorize which geographic location(s) a meta clue might map to?

  • Examples:
    • Brazilian area codes are fairly simple to learn as the first number maps to a region and the second maps to a sub-region within that region while US area codes have no such geographic organization scheme and similarities between the codes themselves essentially have no bearing on the regions where codes are actually used.
  • Theoretical metrics:
    • coherence score = 1 - (entropy of clue→region mapping) - In plain terms: if similar-looking or numerically close clues map to geographically close places, the entropy is lower = higher coherence.

• Frequency of exposure: Meta clues that are uncommon are harder to memorize merely by way of occurring less, making reinforcement and retention difficult.

  • Examples:
    • Some utility pole styles only show up in sparsely populated or under-covered countries, making them tricky to remember even if they’re distinctive.
  • Theoretical metrics:
    • exposure rate = % of games in a given region that contain the clue in question within first X seconds of movement

When choosing to study a meta it’s important to weigh the tradeoff between meta difficulty and expected payoff. Low-difficulty/high-utility metas such as driving sides, hemispheres, road signage, and script and language spotting skills are absolute low-hanging fruit for newer players while more advanced metas like utility poles and bollards carry a higher memorization tax but are practically a necessity to unlocking higher levels of competitive play.

---

Distinctiveness

Distinctiveness refers to how sharply a meta clue narrows down your set of location candidates. In terms of likelihood vectors, a meta clue’s distinctiveness reflects the magnitude of its impact — that is, how strongly the clue shifts the probability toward a specific subset of locations while ruling out others.

Key factors that contribute to a meta’s distinctiveness include:

• Geographic exclusivity: How many regions share the clue, and how large are those regions?

  • Examples:
    • Kangaroos are only found in the wild in Australia, which gives the clue high exclusivity which basically nullifies the possibility for any other country. However, due to Australia’s massive size and the ubiquity of kangaroos throughout the country, their overall exclusivity score is comparatively low.
    • The presence of a flag that only appears in Vatican City or San Marino would carry very high exclusivity due to the extremely small area it applies to.
  • Theoretical metrics:
    • exclusivity = 1 - (sum of area-weighted probabilities of all matching regions)
      (A clue that only applies to a large country like Russia or Canada may still be less distinctive than one that applies to a tiny country or a specific region within a country.)

• Portability: How likely is it for the clue to appear outside of its “home” region?

  • Examples:
    • In Turkey, stop signs are legally mandated to say “Dur,” making it very unlikely to find a standard English “Stop” sign there.
    • The Oscar Mayer Wienermobile may be “native” to the U.S., but it could feasibly be transported elsewhere, reducing its geographic exclusivity.
  • Theoretical metrics:
    • roaming frequency = (# of sightings of the clue outside its home region) ÷ (# of total sightings)
      (Higher = less distinctive)

• Situational Prominence: How often does the clue serve as one of the most important visible clues in a round?

  • Examples:
    • In sparse rural coverage, pole types or road surface patterns may be the best piece of information available.
    • URL domains carry high distinctive weight but are typically found in urban areas where there are often even more distinctive clues available.
    • Theoretical metrics:
      • situational_prominence = # of panoramas where the clue is in the top n most distinctive available clues ÷ # of panoramas where the clue is present

Learning to recognize meta clues with high distinctiveness helps you arrive at more confident guesses more quickly. Advanced players can often confidently make guesses based on just a few, or even just a single, distinctive clue. Prioritizing these metas is especially crucial for No Move and NMPZ play, where every clue carries more weight.

---

Universality

Universality captures how broadly applicable a meta clue is across the total coverage of the game. A highly universal meta provides useful information in a wide range of rounds, while a low-universality meta is only relevant in niche contexts.

• Coverage breadth: How much of the map does this meta apply to?

  • Examples:
    • The driving side meta applies in nearly every country with coverage and is thus highly universal.
    • Kabupaten signs are found throughout Indonesia and provide highly distinctive regional information but they are specific to that country and not very universal.
  • Theoretical metrics:
    • universality score = (area of the regions where a meta is applicable) ÷ (total area of all regions with coverage)

• Ubiquity: How often is the clue physically visible in Street View imagery across regions and round types?

  • Examples:
    • Utility poles and road lines appear frequently across both urban and rural coverage.
    • Top-level domains are rarely visible, even in signage-heavy environments.
  • Theoretical metric:
    • ubiquity = # of panoramas where the clue is visible ÷ total # of panoramas across coverage

Highly universal metas provide a good source of checklist clues, things you can look for that are almost always useful.

---

Stability

Stability measures how consistent, reliable, and long-lasting a meta clue is over time and across updates. Some metas are evergreen; others decay as real-world infrastructure changes, Street View coverage shifts, or Google updates its processing pipeline.

• Temporal consistency: Has the clue remained valid across different eras of coverage?

  • Examples:
    • Language scripts and road line styles tend to be highly stable.
    • The Google car meta is notoriously unstable, changing rapidly and often becoming obsolete with new camera generations.
  • Theoretical metrics:
    • consistency = (# of panos from different generations where a specific clue is present and recognizable) / (Total # of panos)

• Update resistance: How likely is the clue to be present/recognizable in successive generations of Street View coverage?

  • Examples:
    • A specific dog seen in an area is highly unlikely to appear in the next generation of coverage.
    • Most landmarks are consistently and deliberately included in Street View.
  • Theoretical metrics:
    • update resistance = 1 - ((# of previously valid panos where the clue became invalid after an update) / (# of previously valid panos))

• Real-World Volatility: How vulnerable is a clue to real-world changes that might affect its appearance or presence between generations of Street View coverage?

  • Examples:
    • Billboards circulate regularly and are unlikely to remain consistent between generations of coverage.
    • Utility infrastructure tends to remain consistent for decades.
  • Theoretical metrics:
    • volatility = (years of continued reliability / years since clue was first observed) × (inverse of documented exceptions)

Stable metas are great investments: they resist churn and let you build long-term muscle memory without constant relearning while unstable metas might be powerful but susceptible to invalidation over time.